Reading-notes
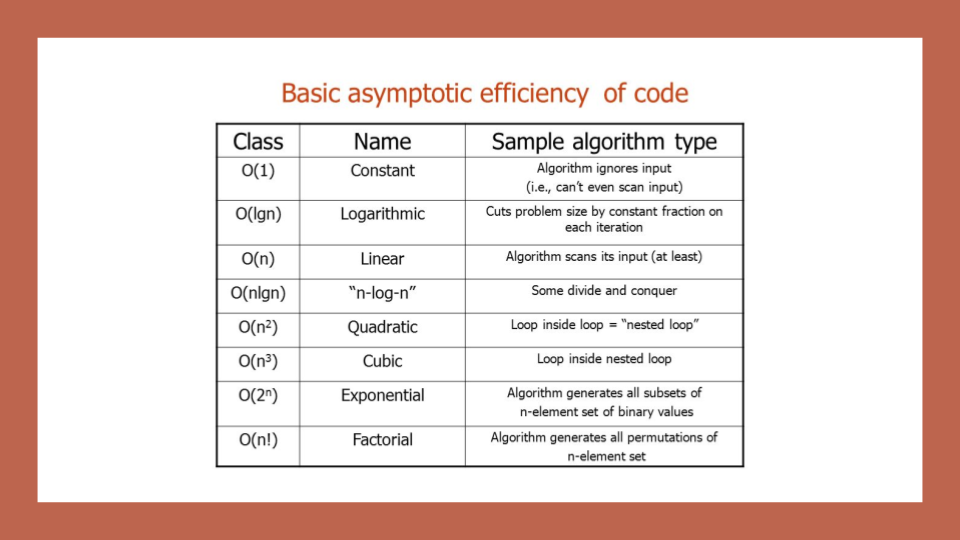
Big O :
Big Omega: This notation describes the Best Case for a given algorithm. The Order of Growth used represents the lower bounds of Time and Space.
Big Theta: This notation describes the Average Case. The Order of Growth used represents the tight bound of Time and Space.
efficiency of an algorithm or function based on 2 factors: describe the Worst Case of efficiency
1-Running Time (also known as time efficiency)
2- Memory Space (also known as space efficiency )
timig
in order to analyze these limiting factors, we should consider 4 Key Areas for analysis:
- Input Size
(size of the parameter values that are read by the algorithm) takes into account the size of each parameter value as well as their numbers) The higher this number, the more likely there will be an increase to Running Time and Memory Space
- Units of Measurement The time in milliseconds(won’t be considering this measurement since different machines will have different individual run times )
-
Orders of Growth( number of lines of code that are executed from start to finish of a function.)
- Best Case, Worst Case, and Average Case (peration that is contributing the most to the total running time. )
Space
1-The amount of space needed to hold the code for the algorithm 2-The amount of space needed to hold the input data 3-The amount of space needed for the output data. 4-he amount of space needed to hold working space during the calculation
Orders of Growth
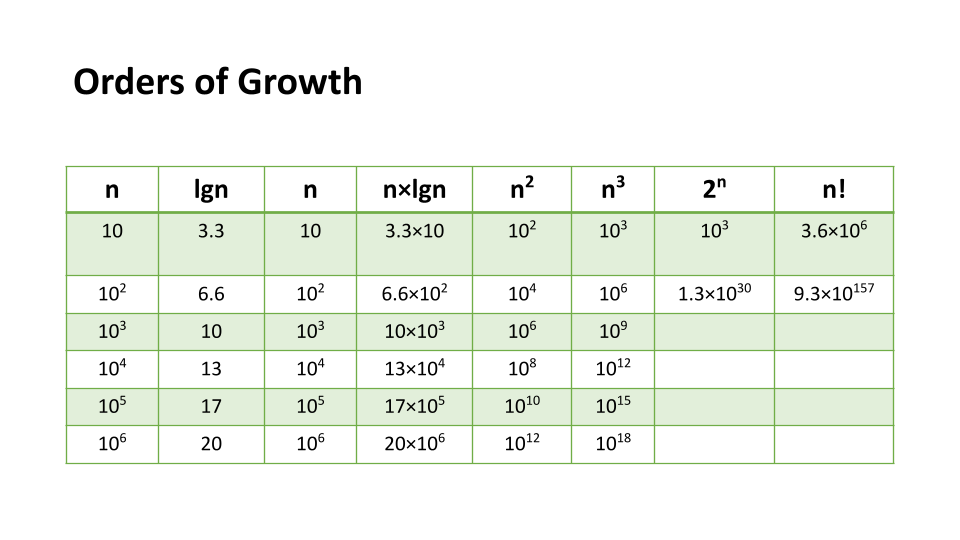
Constant Complexity means that no matter what inputs are thrown at our algorithm, it always uses the same amount of time or space. T
Logarithmic Complexity represents a function that sees a decrease in the rate of complexity growth, the greater our value of n.
** Linear Complexity, the size of our inputs ‘n’ will directly determine the amount of Memory Space used and Running Time length.**
Linearithmic Complexity is used to describe a growth rate of n by lgn
Quadratic Complexity describes an algorithm with complexity growing at a rate of input size n multiplied by n
Cubic Complexity is typically just a higher degree of what makes the quadratic complexity grow at such a high rate
Exponential Complexity represents very rapidly growing complexity, such that whatever our input size
Worst Case: The efficiency for the worst possible input of size n
Best Case: The efficiency for the best possible input of size n
Average Case: The efficiency for a “typical” or “random” input of size n.
Linked list
The fundamental difference between arrays and linked lists is that arrays are static data structures, while linked lists are dynamic data structures.
dynamic data structure can shrink and grow in memory.
Parts of a linked list
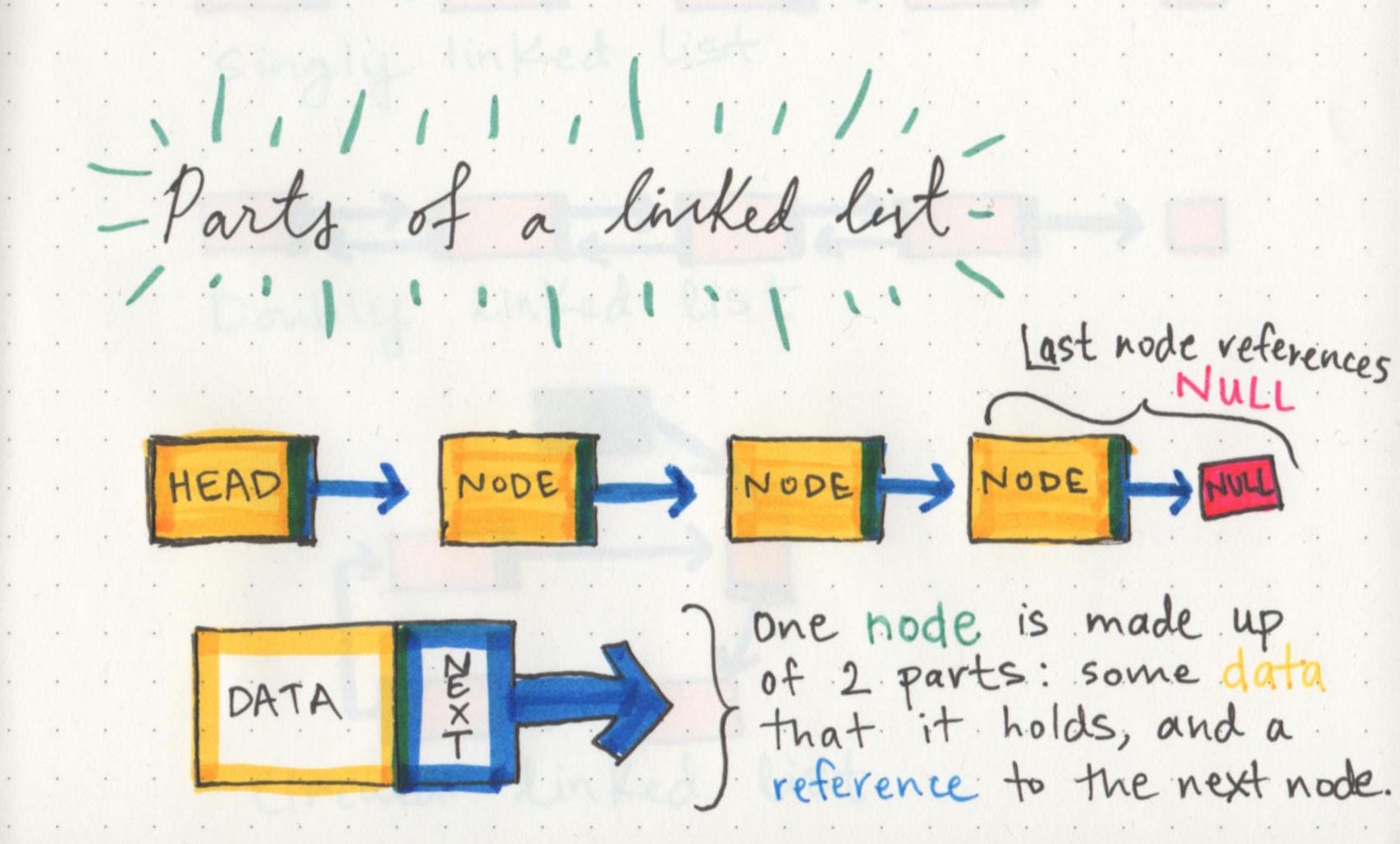A linked list is made up of a series of nodes, which are the elements of the list.
head:starting point of the list is a reference to the first node.
single node : It has just two parts: data, or the information that the node contains, and a reference to the next node.
A node only knows about what data it contains, and who its neighbor is.
**A single node doesn’t know how long the linked list is. **
Lists for all shapes and sizes
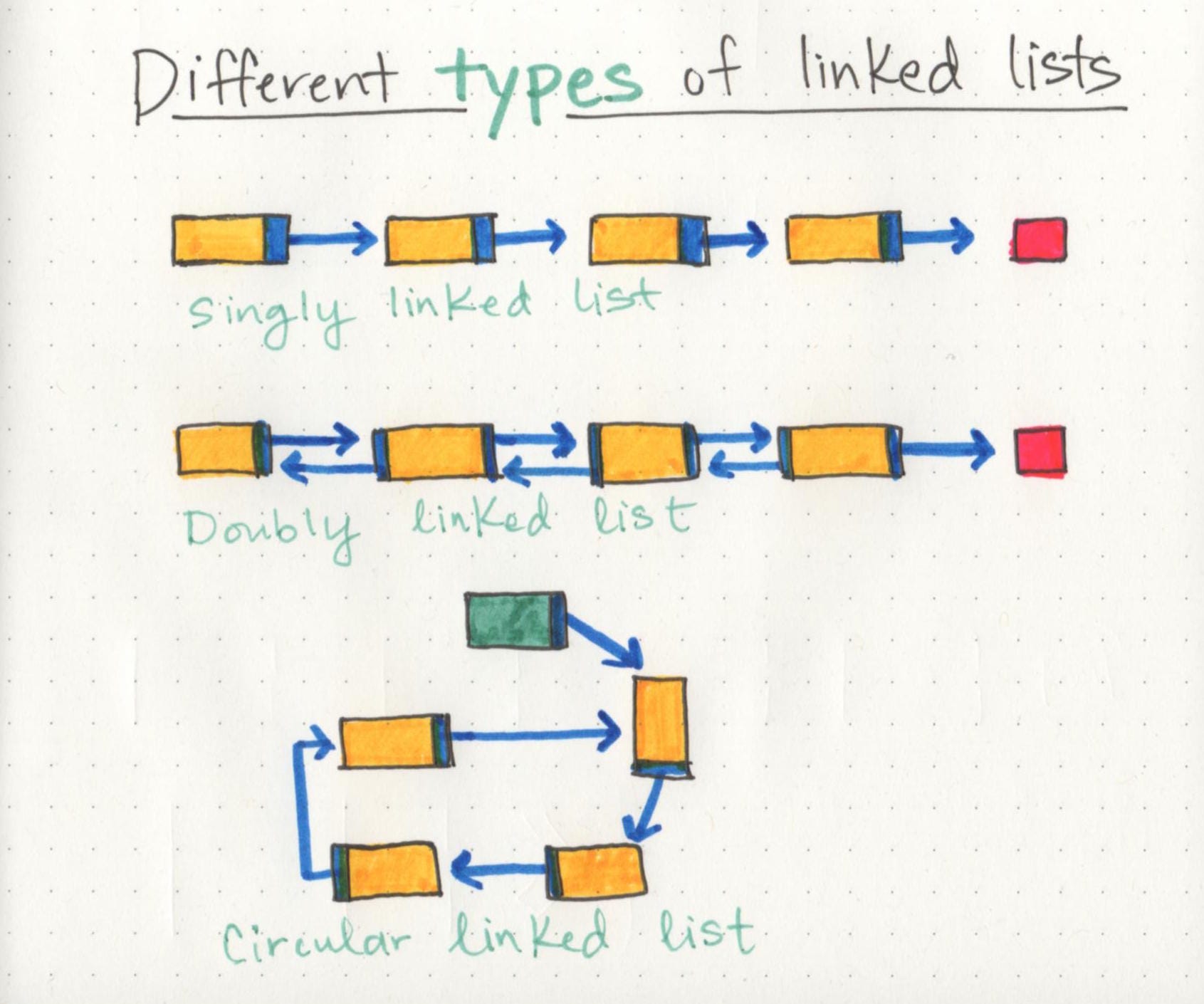
Singly linked lists are the simplest type of linked list, based solely on the fact that they only go in one direction
This is what we call a doubly linked list, because there are two references contained within each node: a reference to the next node, as well as the previous node.
** circular linked list is a little odd in that it doesn’t end with a node pointing to a null value. **
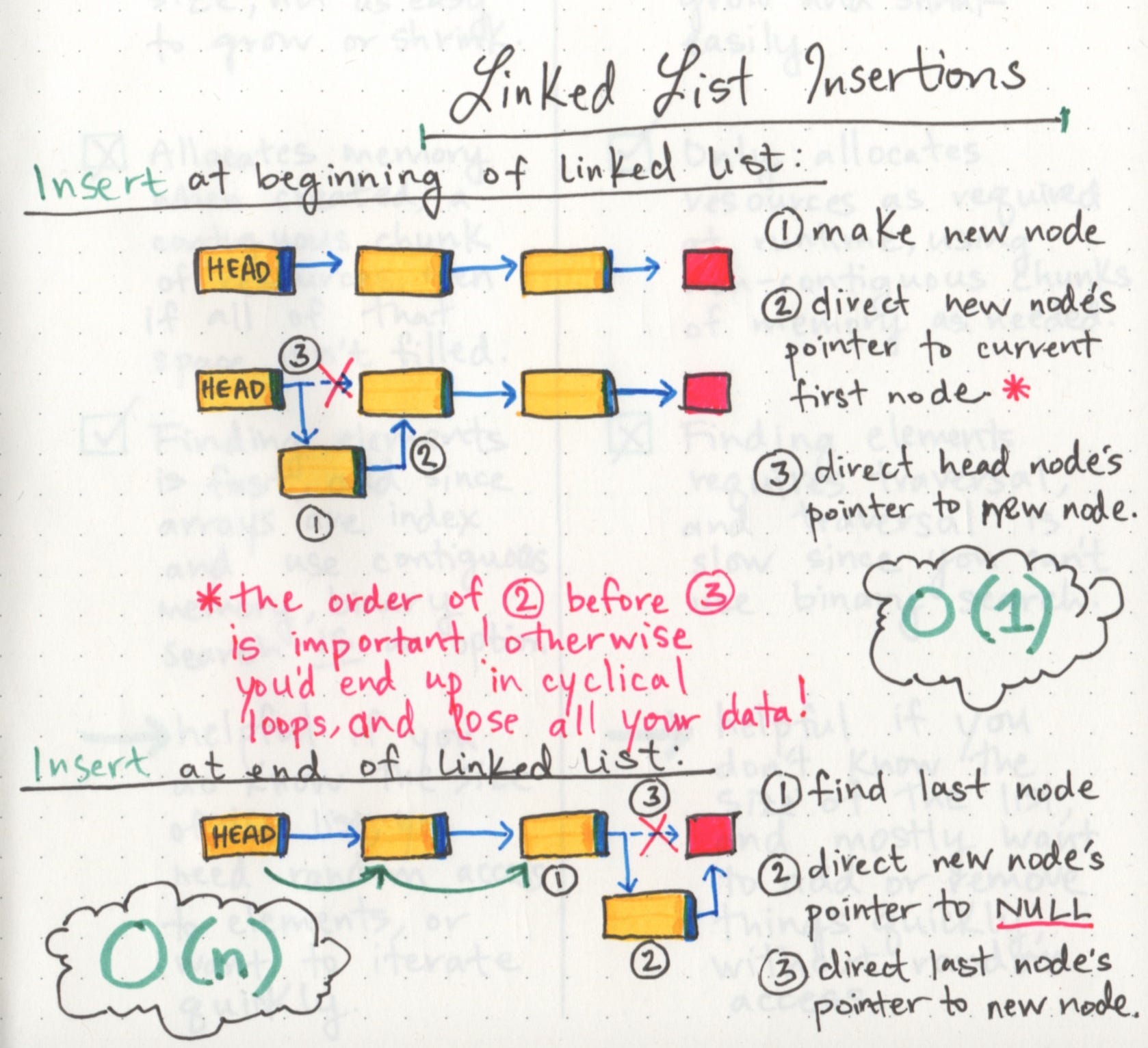
Growing a linked list
we can add elements and remove elements from a linked list. But unlike arrays, we don’t need to allocate memory in advance or copy and re-create our linked list, since we won’t “run out of space” the way we might with a pre-allocated array.
First we find the head node of the linked list.
Next we’ll make our new node, and set its pointer to the current first node of the list.
Lastly we rearrange our head node’s pointer to point at our new node.
a linked list is usually efficient when it comes to adding and removing most elements, but can be very slow to search and find a single element.
