Reading-notes

Graphs

A graph is a non-linear data structure that can be looked at as a collection of vertices (or nodes) potentially connected by line segments named edges.

• Vertex - A vertex, also called a “node”, is a data object that can have zero or more adjacent vertices.
• Edge - An edge is a connection between two nodes.
• Neighbor - The neighbors of a node are its adjacent nodes, i.e., are connected via an edge.
• Degree - The degree of a vertex is the number of edges connected to that vertex.

Undirected Graphs

An Undirected Graph is a graph where each edge is undirected or bi-directional. This means that the undirected graph does not move in any direction

Vertices/Nodes = {a,b,c,d,e,f}

Edges = {(a,c),(a,d),(b,c),(b,f),(c,e),(d,e),(e,f)}

Directed Graphs (Digraph)

A Directed Graph also called a Digraph is a graph where every edge is directed.

Unlike an undirected graph, a Digraph has direction. Each node is directed at another node with a specific requirement of what node should be referenced next.

Vertices = {a,b,c,d,e,f}

Edges = {(a,c),(b,c),(b,f),(c,e),(d,a),(d,e)(e,c)(e,f)}

Complete Graphs

A complete graph is when all nodes are connected to all other nodes.

Connected

A connected graph is graph that has all of vertices/nodes have at least one edge.

Disconnected

A disconnected graph is a graph where some vertices may not have edges.

cyclic Graph

An acyclic graph is a directed graph without cycles.

A cycle is when a node can be traversed through and potentially end up back at itself.

Here is an example of 3 acyclic graphs:

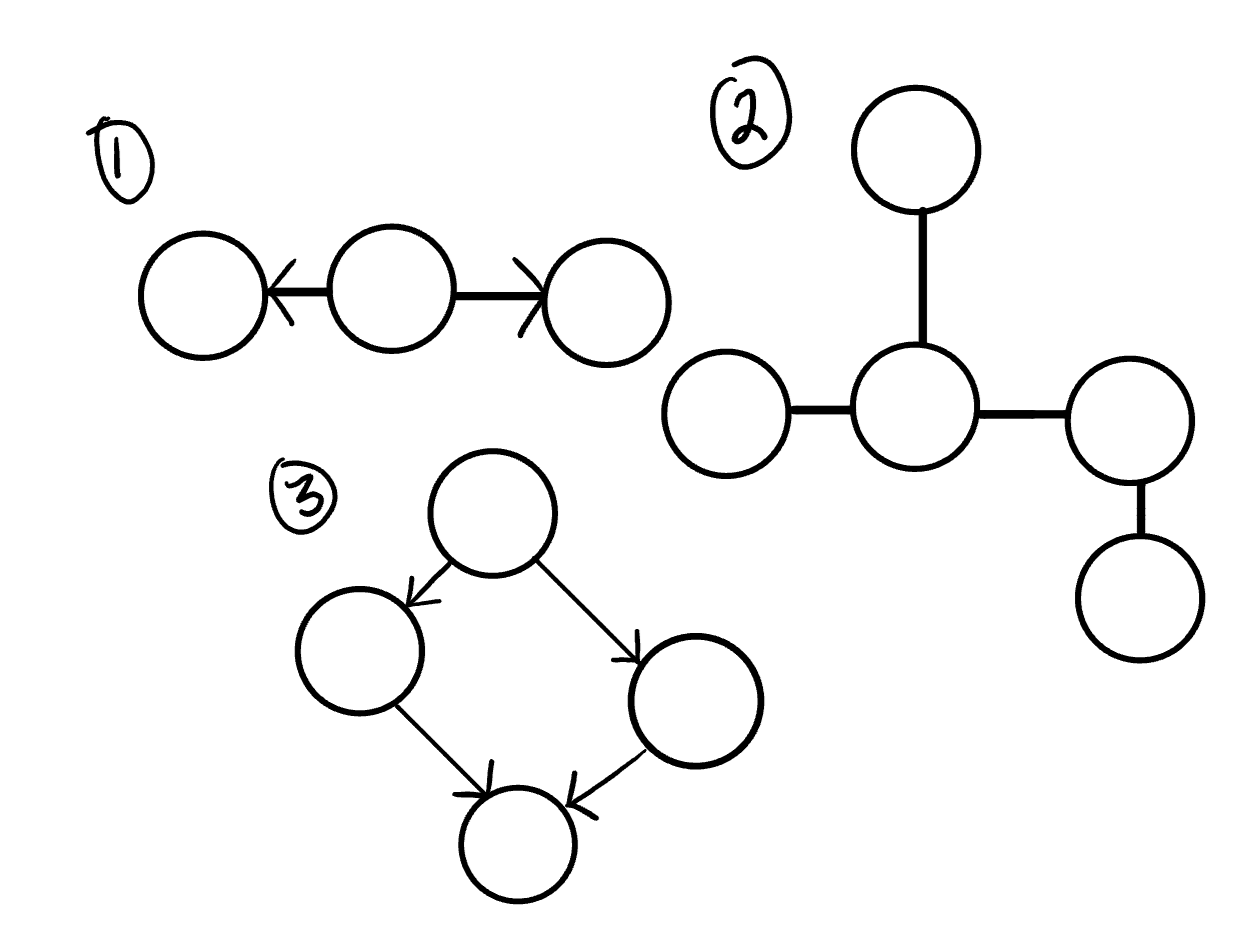
Cyclic Graphs

A Cyclic graph is a graph that has cycles.

A cycle is defined as a path of a positive length that starts and ends at the same vertex.

Here is an example of a two different cyclic graph:

Graph Representation

Adjacency Matrix

An Adjacency matrix is represented through a 2-dimensional array. If there are n vertices, then we are looking at an n x n Boolean matrix

Each Row and column represents each vertex of the data structure. The elements of both the column and the row must add up to 1 if there is an edge that connects the two, or zero if there isn’t a connection.

Adjacency List

An adjacency list is a collection of linked lists or array that lists all of the other vertices that are connected.

Adjacency lists make it easy to view if one vertices connects to another.

Weighted Graphs

A weighted graph is a graph with numbers assigned to its edges. These numbers are called weights. This is what a weighted graph looks like:

Using the graph from above, here is an example of what a weight matrix would look like:

Traversals

In a breadth first traversal, you are starting at a specific vertex/node. This node must be specified when calling the BreadthFirst() method. The breadth-first traversal of a graph is like that of a tree, with the exception that graphs can have cycles.

Here is what the algorithm breadth first traversal looks like:

• Enqueue the declared start node into the Queue.
• Create a loop that will run while the node still has nodes present.
• ` Dequeue` the first node from the queue
• if the Dequeue‘d node has unvisited child nodes, add the unvisited children to visited set and insert them into the queue.

Depth First

• Push the root node into the stack
• Start a while loop while the stack is not empty

• Peek at the top node in the stack If the top node has unvisited children, mark the top node asvisited, and then Push any unvisited children back into the stack.

• If the top node does not have any unvisited children, Pop that node off the stack
• repeat until the stack is empty.

graphs in use:

• GPS and Mapping
• Driving Directions
• Social Networks
• Airline Traffic
• Netflix uses graphs for suggestions of products

resources